Using Deep Q-Network to Learn How To Play Flappy Bird - 解釋 
該程式是透過Reinforcement Learning的方式,經由Convolutional neural network從模擬器(螢幕上)讀取畫面,讀取該遊戲情態(s0),並由Deep neural network分析執行相對應的動作(a),觀察所得的獎勵(r),並取得下一個情態(s1)。 上述整個流程就是一個典型的Markov decision process(MDP),用一個Convolutional neural network(CNN)來實現,然則和典型CNN不同的是Cost function是由Bellman Equation對整個Neural network做更新。
以下用Pseudo-code對整個流程做解釋:

模型流程圖示: 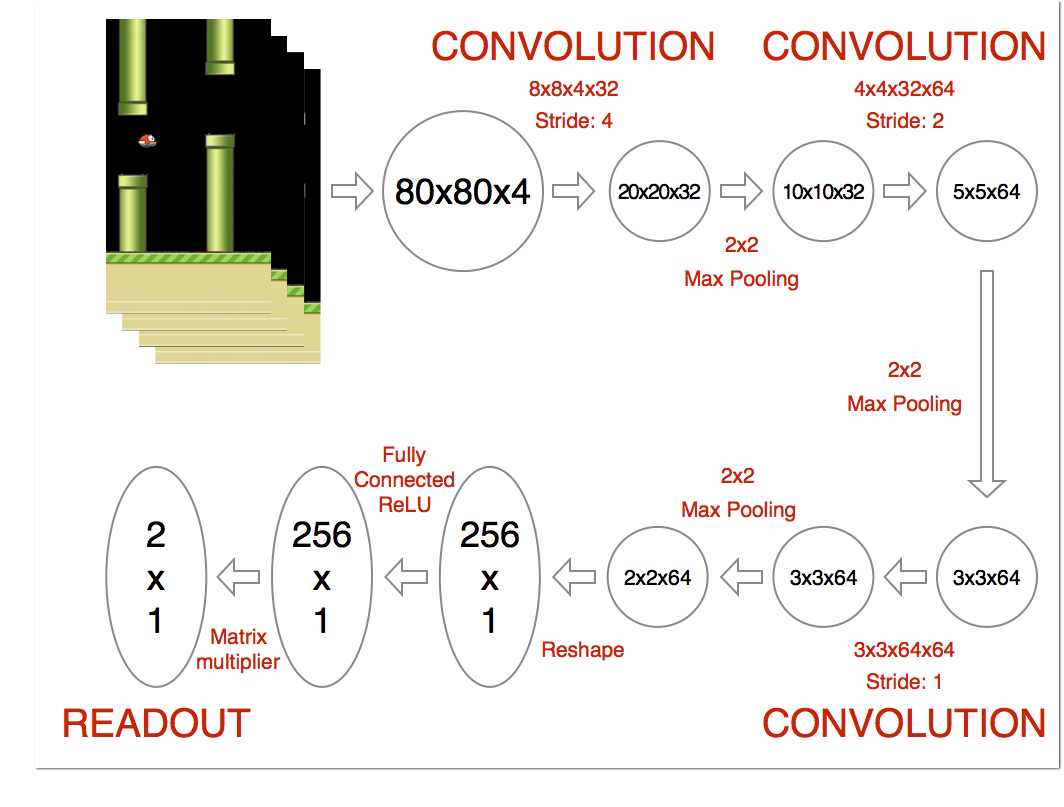
DEMO:
7mins demo for DQN play flappy bird
接下來針對程式碼執行訓練Network的部分做較詳細的解釋: 詳細請參考:deep_q_network.py
def trainNetwork(s, readout, h_fc1, sess):
# define the cost function
#定義cost function,採最小平方法訓練
a = tf.placeholder("float", [None, ACTIONS])
y = tf.placeholder("float", [None])
readout_action = tf.reduce_sum(tf.mul(readout, a), reduction_indices=1)
cost = tf.reduce_mean(tf.square(y - readout_action))
train_step = tf.train.AdamOptimizer(1e-6).minimize(cost)
# open up a game state to communicate with emulator
#初始遊戲
game_state = game.GameState()
# store the previous observations in replay memory
#定義一個Queue放replayMemory
D = deque()
# printing
#log存放處
a_file = open("logs_" + GAME + "/readout.txt", 'w')
h_file = open("logs_" + GAME + "/hidden.txt", 'w')
# get the first state by doing nothing and preprocess the image to 80x80x4
#初始第一個動作
do_nothing = np.zeros(ACTIONS)
#將動作定義為不做任何事
do_nothing[0] = 1
#將動作輸入至遊戲,並取得其後的螢幕和reward
x_t, r_0, terminal = game_state.frame_step(do_nothing)
#將取得遊藝螢幕轉換做灰階
x_t = cv2.cvtColor(cv2.resize(x_t, (80, 80)), cv2.COLOR_BGR2GRAY)
ret, x_t = cv2.threshold(x_t,1,255,cv2.THRESH_BINARY)
#轉換成situation格式
s_t = np.stack((x_t, x_t, x_t, x_t), axis=2)
# saving and loading networks
#儲存模型
saver = tf.train.Saver()
#初始化模型
sess.run(tf.initialize_all_variables())
checkpoint = tf.train.get_checkpoint_state("saved_networks")
#假若要重新training一個model則42-46需註解掉
if checkpoint and checkpoint.model_checkpoint_path:
saver.restore(sess, checkpoint.model_checkpoint_path)
print("Successfully loaded:", checkpoint.model_checkpoint_path)
else:
print("Could not find old network weights")
# start training
epsilon = INITIAL_EPSILON
t = 0
while "flappy bird" != "angry bird":
# choose an action epsilon greedily
#將螢幕的situation喂到NN取得Q值
readout_t = readout.eval(feed_dict={s : [s_t]})[0]
#初始動作的array
a_t = np.zeros([ACTIONS])
action_index = 0
if t % FRAME_PER_ACTION == 0:
#初始時隨機選擇一個動作機會較大,但隨著Training時間越久而逐漸降低
if random.random() <= epsilon: print("----------Random Action----------") #隨機選擇一個動作 action_index = random.randrange(ACTIONS) a_t[random.randrange(ACTIONS)] = 1 else: #選取Q較大的值當作下步動作 action_index = np.argmax(readout_t) a_t[action_index] = 1 else: 非判斷的Frame則不動作 a_t[0] = 1 # do nothing # scale down epsilon 降低掉入隨機存取的機率 if epsilon > FINAL_EPSILON and t > OBSERVE:
epsilon -= (INITIAL_EPSILON - FINAL_EPSILON) / EXPLORE
# run the selected action and observe next state and reward
#執行所選取的動作
x_t1_colored, r_t, terminal = game_state.frame_step(a_t)
#將執行後的畫面轉成灰階
x_t1 = cv2.cvtColor(cv2.resize(x_t1_colored, (80, 80)), cv2.COLOR_BGR2GRAY)
ret, x_t1 = cv2.threshold(x_t1, 1, 255, cv2.THRESH_BINARY)
#將畫面壓成80*80大小
x_t1 = np.reshape(x_t1, (80, 80, 1))
#s_t1 = np.append(x_t1, s_t[:,:,1:], axis = 2)
#轉換成Situation格式
s_t1 = np.append(x_t1, s_t[:, :, :3], axis=2)
#將執行過程中所產生的Situation,action,reward,下個situation存入Replay memory
# store the transition in D
D.append((s_t, a_t, r_t, s_t1, terminal))
#若Replaymemory超過指定大小則拿掉最舊的memory
if len(D) > REPLAY_MEMORY:
D.popleft()
#當完成Observing才做訓練模型的動作,也就是前100000步都亂玩,只為了記錄Situation
if t > OBSERVE:
# sample a minibatch to train on
#根據Batch隨機選取sample來做training
minibatch = random.sample(D, BATCH)
#轉會成要training的格式
# get the batch variables
s_j_batch = [d[0] for d in minibatch]
a_batch = [d[1] for d in minibatch]
r_batch = [d[2] for d in minibatch]
s_j1_batch = [d[3] for d in minibatch]
y_batch = []
#將螢幕的Situation喂到NN裡並取得他的Q值,這裡要注意的是是每筆Memory中的situation執行完action後的St+1
readout_j1_batch = readout.eval(feed_dict = {s : s_j1_batch})
for i in range(0, len(minibatch)):
terminal = minibatch[i][4]
# if terminal, only equals reward
if terminal:
#若為終局則直接做輸出
y_batch.append(r_batch[i])
else:
#如果未到Terminal則根據bellman equation更新
y_batch.append(r_batch[i] + GAMMA * np.max(readout_j1_batch[i]))
#開始訓練
# perform gradient step
train_step.run(feed_dict = {
y : y_batch,
a : a_batch,
s : s_j_batch}
)
# update the old values
s_t = s_t1
t += 1
# save progress every 10000 iterations
#每一萬步儲存一次訓練模型
if t % 10000 == 0:
saver.save(sess, 'saved_networks/' + GAME + '-dqn', global_step = t)
# print info
state = ""
if t <= OBSERVE: #觀察中,也就是前100000步 state = "observe" elif t > OBSERVE and t <= OBSERVE + EXPLORE:
#100000~2100000訓練
state = "explore"
else:
state = "train"
print("TIMESTEP", t, "/ STATE", state, \
"/ EPSILON", epsilon, "/ ACTION", action_index, "/ REWARD", r_t, \
"/ Q_MAX %e" % np.max(readout_t))
# write info to files
'''
if t % 10000 <= 100:
a_file.write(",".join([str(x) for x in readout_t]) + '\n')
h_file.write(",".join([str(x) for x in h_fc1.eval(feed_dict={s:[s_t]})[0]]) + '\n')
cv2.imwrite("logs_tetris/frame" + str(t) + ".png", x_t1)
'''
額外補充:
1.該學習方法稱為Off-Policy Learning,既然有Off,那On是否存在?其稱為On-Policy Learning!之後會有另外的文章做介紹。
2.早期在做Reinforcement Learning時,學習的方式是採用更新Q-Table的方式,什麼是Q-Table呢?想像情態和動作的多種組合,假設情態只發生兩種,動作也只有兩種,那可以有的組合為2X2=4種可能,在訓練過程當中,我們更新這4個組合的Q-Value值,讓整個模型學習在既定的狀態下做出最適合的動作,這其實非常容易!而另外的例子,我們依然假設動作只有兩種,但情態推廣到如Flappy Bird有那麼多種,電腦在初始記憶體大小時得要準備多少空間?於是我們將Q-Table抽換掉,將Deep Neural network(DNN)(或稱Q-Neural network)置入,讓DNN學習在某些情境,該採取什麼樣的動作,以取代如此高維度的空間。但缺點是這中間仰賴極大的運算,而近年因為GPU運算成本降低,該方法得到良好的推廣。 參考: 1.DeepLearningFlappyBird 2.artint.info-11.3.3 Q-learning